Improved density functional theory method gets band gaps right

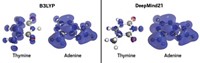
A popular quantum mechanical method for calculating the properties of molecules and solid materials has routinely underestimated the size of semiconductor band gaps. A new version of that computational method developed by University of Minnesota researchers is now showing marked improvement in calculating band gap values without sacrificing the method’s speed and simplicity (J. Phys. Chem. Lett. 2016, DOI: 10.1021/acs.jpclett.6b02757). Band gaps represent the energy difference between a material’s valence and conduction electron bands, with the magnitude making the difference between conductors, insulators, and semiconductors. Researchers have long used the Kohn-Sham form of density functional theory (KS-DFT) to investigate electron band structures, excitation energies, and other fundamental properties. One version of KS-DFT relies on so-called local functionals—mathematical descriptions of electron density—and is popular because its simplicity offers substantial computational cost savings relative to other quantum methods. But local functional programs tend to miss the mark on band gaps, forcing researchers to refine their work using computationally-intensive methods based on nonlocal functionals. Pragya Verma and Donald G. Truhlar developed a local functional, called HLE16, and tested it on 31 semiconductors. They find that it yields more accurate band-gap estimates than current local functionals and matches the low-error values of the most popular nonlocal functionals.